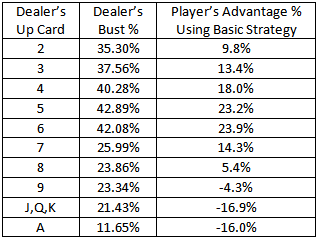
The most important frequencey to note is the chance of being dealt a natural blackjack (natural 21 value. The odds of being dealt a natural blackjack are merely 4.8%. Following this chart you will see that the most common two card hand, at 38.7%, is a hand totaling 1-16, which is considered a decision hand. Dealer Final Hand Probabilities. Without any deeper understanding of odds in blackjack, it’s easy to believe that hitting on a hand value of 12 would always be the right decision. This is because 12 is a very low value and the fact that more than two-thirds of the cards in the deck (s) would improve the value of it.

Did you know that you can play more than one hand of blackjack at a time in most casinos?

If a table is full, this isn’t possible. But at most casinos, the blackjack tables aren’t quite full. I see a lot of my fellow gamblers playing two hands simultaneously. You’re not limited to just two hands either. You could even play three hands at the same time if you needed to.

Is this a good idea or not? A simple answer might be to think about what playing multiple hands does to your average win or loss rate.

If you’re a recreational player, even if you use basic strategy, playing multiple hands simultaneously just means you’ll lose more money faster. But if you’re an advantage blackjack player, playing multiple hands simultaneously will result in a higher average hourly win rate.

If you’re thinking about playing two hands at a time instead of just one, you should examine your reasoning for this rationally. If you think it’s just going to change your luck, you shouldn’t do it. The number of hands you’re playing doesn’t affect luck in any way because, after all, luck is just standard deviation.

The house edge will stay the same regardless of how many hands you’re playing.

What Playing Multiple Hands Does

Let’s look at a few different scenarios.

In the first scenario, you decide to play one hand at a time for $5 per hand. You’re using perfect basic strategy, and the house edge in this specific casino is only 0.4%. It’s a two-deck game with good rules. It’s also the middle of the afternoon, and the casino isn’t busy, so you’re playing heads up against the dealer. This means you’re getting in 200 hands per hour.

The amount you’re mathematically expected to lose in this scenario is easy to calculate. You multiply the number of bets you’re making per hour (200) by their size ($5) to get your total amount of hourly action.

In this case, you’re putting $1000 into action per hour. The house edge is the amount the casino expects to win in the long run, so you multiply the house edge by the action. That gives you an expected hourly loss of $4.

Now, let’s take a second scenario. It’s the same table, same rules, same amount per hand, and same perfect strategy on your part.

But because you’re playing two hands per hour, the game slows down a little bit to 160 hands per hour, but multiplied by 2, since you’re playing both of them.

Now, you’re getting in 320 hands per hour, which means your hourly action jumps to $1600. 0.4% of $1600 is $6.40 per hour in expected losses. It’s obvious that you’re going to lose more money playing two hands per hour.

Also, the more hands you get in, the closer your actual results will get to the mathematically expected results. In other words, if you’re hoping to capitalize on a short-term lucky streak, you reduce the probability of doing that by playing so many hands.

Now, let’s look at a third scenario. You’re playing the same game, but you’re counting cards, and you have a 0.4% edge over the house instead of playing against a house edge of 0.4%.

Instead of an expected loss per hour of $4, you now have an expected win per hour of $4. AND if you play two hands instead of one, you have an expected win per hour of $6.40.

Since you’re counting cards, you get more information faster by seeing more cards per hand, too. The more cards you see, the more accurate your count becomes.

One More Example of Playing Multiple Blackjack Hands at Once

I want to look at one more scenario. This time, instead of playing for $5 per hand, you have a player who’s
betting $100 per hand.

That’s 200 hands per hour at $100 per hand, or $20,000 in hourly action. 0.4% of that is $80 in expected losses per hour.

What if this player decides to start playing two hands at a time instead of just one, and he only bets $50 per hand? He’s still putting $100 “per round” into action, but the action slows down because of the extra hands.

Instead of 200 bets per hour at $100, he’s getting in 320 bets per hour in at $50 per hand, or $16,000 in hourly action. His hourly expected loss goes down to $64 instead of $80.

If this player were counting cards with an edge of 0.4%, his hourly win rate would drop correspondingly. This seems counterintuitive, but if you think about it, this is the case.

Some Conclusions to Draw From All this Math

The first conclusion is that if you’re not changing the size of your bets, but you’re making almost twice as many bets per hour, you’ll lose (or win) more money based on your mathematical expectation. Average players will lose more per hour, and advantage players will win more per hour.

But if you reduce the size of your bets AND reduce the number of hands you’re getting per hour, you’ll lose (or win) more money, again based on your mathematical expectation.

Most of my readers are basic blackjack strategy players. This means that, over time, they’re going to see a net loss. But that net loss is lower than you’d see at almost any game in the casino.

My hope for that player would be that they’d realize the importance of getting in fewer hands per hour. The fewer hands you play per hour, the less money you’ll lose on average over time.

Playing two hands at once is one way to get in fewer hands per hour, but it’s not the only way. You could also limit your play to tables with a minimum number of players.

If you stick with games where there were at least four other players at the table, you’d only play 70 hands per hour instead of 200 or 160. You could afford to bet more per hand and still lose less money per hour at such a table.

And if you stick with your other betting amounts, you’d save a lot of money and have a lot of fun socializing while you’re at it.

Conclusion

The pros of playing multiple hands of blackjack at the same time are simple enough.

• If you have an edge over the casino, you can make more money per hour doing this.
• If you don’t, you can put the same amount of money into play per round by playing two hands instead of one and betting half the amount. This will reduce your hourly expected loss rate.

The cons of playing multiple hands of blackjack are simple enough, too.

• You’re less likely to see a lucky winning streak based on short term variance.
• You’re going to lose more money per hour if you don’t reduce your bet size, because you’ll be getting in more hands per hour for the same amount per hand.

Should you play multiple hands of blackjack simultaneously? That depends on all the factors discussed above.

Are you a card counter? Do you think you’ll try to earn more by playing two hands at a time after reading this? Are you a basic strategy player? Do you think you’ll try to get in less action per hour to try to reduce your hourly loss rate?

Let me know in the comments.

Please enable JavaScript to view the comments powered by Disqus.

We first present the probabilities attached to card dealing and initial predictions. In making this calculus, circumstantial information such as fraudulent dealing is not taken into account (as in all situations corresponding to card games). All probabilities are calculated for cases using one or two decks of cards. Let us look at the probabilities for a favorable initial hand (the first two cards dealt) to be achieved. The total number of possible combinations for each of the two cards is C(52, 2) = 1326, for the 1-deck game and C(104, 2)=5356for the 2-deck game.

Probability of obtaining a natural blackjack isP= 8/663 = 1.20663% in the case of a 1-deck game andP = 16/1339 = 1.19492%in the case of a 2-deck game.

Probability of obtaining a blackjack from the first two cards isP= 32/663 = 4.82654%in the case of a 1-deck game andP = 64/1339= 4.77968%in the case of a 2-deck game.

Similarly, we can calculate the following probabilities:

Probability of obtaining 20 points from the first two cards isP = 68/663 = 10.25641% in the case of a 1-deck game andP= 140/1339 = 10.45556%in the case of a 2-deck game.

Probability of obtaining 19 points from the first two cards isP = 40/663 = 6.03318%in the case of a 1-deck game andP = 80/1339 = 5.97460%in the case of a 2-deck game.

Probability of obtaining 18 points from the first two cards isP= 43/663 = 6.48567%in the case of a 1-deck game andP= 87/1339 = 6.4973% in the case of a 2-deck game.

Probability of getting 17 points from the first two cards isP= 16/221 = 7.23981%in the case of a 1-deck game andP= 96/1339 = 7.16952%in the case of a 2-deck game.

A good initial hand (which you can stay with) could be a blackjack or a hand of 20, 19 or 18 points. The probability of obtaining such a hand is calculated by totaling the corresponding probabilities calculated above: P = 32/663 + 68/663 + 40/663 + 43/663 = 183/663, in the case of a 1-deck game and P = 64/1339 + 140/1339 + 80/1339 + 87/1339 = 371/1339, in the case of a 2-deck game.

Probability of obtaining a good initial hand isP= 183/663 = 27.60180%in the case of a 1-deck game andP= 371/1339 = 27.70724%in the case of a 2-deck game.

The probabilities of events predicted during the game are calculated on the basis of the played cards (the cards showing) from a certain moment. This requires counting certain favorable cards showing for the dealer and for the other players, as well as in your own hand. Any blackjack strategy is based on counting the cards played. Unlike a baccarat game, where a maximum of three cards are played for each player, at blackjack many cards could be played at a certain moment, especially when many players are at the table. Thus, both following and memorizing certain cards require some ability and prior training on the player’s part. Card counting techniques cannot however be applied in online blackjack.

The formula of probability for obtaining a certain favorable value is similar to that for baccarat and depends on the number of decks of cards used. If we denote by x a favorable value, by nx the number of cards showing with the value x (from your hand, the hands of the other players and the face up card in the dealer’s hand) and by nv the total number of cards showing, then the probability of the next card from the deck (the one you receive if you ask for an additional card) having the value x is:

This formula holds for the case of a 1-deck game. In the case of a 2-deck game, the probability is:

Generally speaking, if playing with m decks, the probability of obtaining a card with the value x is:

Odds Of Poker Hands One Decks

Example of application of the formula: Assume play with one deck, you are the only player at table, you hold Q, 2, 4, A (total value 17) and the face up card of the dealer is a 4. Let us calculate the probability of achieving 21 points (receiving a 4).

We havenx = 2, nv = 5, so:

.

For the probability of achieving 20 points (receiving a 3), we havenx = 0, nv = 5, so:

Odds Of Poker Hands 9 Person Table

.

For the probability of achieving 19 points (receiving a 2), we havenx = 1, nv = 5, so:

Odds Of Losing Consecutive Blackjack Hands

.

If we want to calculate the probability of achieving 19, 20 or 21 points, all we must do is total the three probabilities just calculated. We obtainP = 9/47 = 19.14893%.

Unlike in baccarat, where fewer cards are played, the number of players is constant (two), and the number of gaming situations is very limited, in blackjack, the number of possible playing configurations is in the thousands and, as a practical matter, cannot be entirely covered by tables of values.

Odds Of Poker Hands Artwork

Sources

A big part of the gaming situations that require a decision, where the total value held is 15, 16, 17, 18, 19 or 20 points, is comprised in tables in the section titled Blackjack of the book PROBABILITY GUIDE TO GAMBLING: The Mathematics of Dice, Slots, Roulette, Baccarat, Blackjack, Poker, Lottery and Sport Bets.You will also find there other issues of probability-based blackjack strategy . See the Books section for details.